Hartree Fellow Cultivates New Perspectives on Quantum Computing
Hartree Fellow Cultivates New Perspectives on Quantum Computing

Quantum computers are heralded as promising tools for performing computations that are beyond the reach of supercomputers and every other technology currently at our disposal. But we are in the early days of quantum computing, and there are still basic questions left to answer: How do you know that a clever programmer won’t develop a revolutionary method that allows traditional computers to run circles around the upstart quantum newcomers? And if a quantum computer has solved a problem that no other available technology can, how can you be sure that it’s even right?
Dominik Hangleiter, one of the newest Hartree Postdoctoral Fellows at the Joint Center for Quantum Information and Computer Science (QuICS), develops theoretical frameworks to address these questions and to identify problems at which quantum computers can be proven to dominate.
“This work is especially pressing because the quantum devices that we have at the moment are very faulty and noisy and you can't really trust them,” says Hangleiter. “So I'm working on methods to assess whether you can trust your quantum computer, and also to assess in which situations it's even possible to devise such methods.”
Quantum computers weren’t what attracted Hangleiter to studying physics. In fact, as an undergraduate at the University of Konstanz in Germany, he had little interest in computers. Instead, he studied condensed matter physics (the physics of how interacting particles determine the properties of materials) and the ways quantum physics naturally plays out in materials.
“I'm surprised that I ended up doing very computer sciencey things because I don't really like to interact with computers,” says Hangleiter.
But as a master’s student at Ludwig Maximilian University of Munich, he became interested in the more theoretical and mathematical side of physics and that drew him into the topic of computer science. He began performing research with Jens Eisert, who studies quantum information theory and condensed matter theory, on how to confirm that a quantum simulation worked correctly. He then continued his doctoral research with Eisert at the Free University of Berlin and dug deeper into the topic’s theoretical roots.
As a graduate student, Hangleiter investigated quantum approaches to sampling tasks, a general class of computations that produce random results according to some probability distribution. Since quantum mechanics is fundamentally probabilistic (you can never definitively predict certain individual results beforehand no matter how much information you have), any quantum computer simulating a quantum experiment or performing a purely quantum computation will be a sampling problem. Even though these tasks’ outputs can’t be definitively predicted, they reflect the reality of how quantum mechanics dictates the probability of different outcomes. This intrinsic reflection of quantum probabilities makes these tasks one of the most promising ways to prove that there are computations where quantum computers can significantly outperform traditional computers.
When investigating topics like sampling tasks, Hangleiter often keeps an additional layer of mathematical abstraction between him and the particular approaches—algorithms—that computer scientists have proposed. That mathematical abstraction is complexity theory, which classifies computational tasks based on their resource requirements (the time to run a program, the size of the required circuit, etc.); it serves as a lens to help get an overarching perspective of the mathematical landscape so researchers can avoid blind alleys and spot promising research routes for more thorough exploration. This more abstract approach allows identification of underlying truths about whole styles of approaches instead of getting caught in the weeds of the peculiarities of an individual algorithm.
“In computer science, there's always this problem when you talk about the time it takes you to solve a problem, that you might have just had a bad idea, and someone else might come up with a better algorithm,” says Hangleiter. “So this is what complexity theory is about. It's all about putting problems into classes where we have very strong beliefs that they have genuinely different complexities—you would really require different orders of magnitude of runtime to solve tasks in different classes.”
Hangleiter and his colleagues used this approach in a paper they published in the journal Physical Review Letters when Hangleiter was a doctoral student. They provided strong new evidence that quantum simulations can perform certain sampling tasks that classical computers just aren’t cut out for. In particular, they studied certain quantum simulations with a repeating grid layout. (Specifically, they studied what computer scientists call Hamiltonian quantum simulation architectures that are 2D translation-invariant and have a constant depth.)
“We looked at one type of a sampling scheme for quantum advantage,” says Hangleiter. “Previously, we had proposed this type of task and argued that it's an interesting task because you can potentially do it in present experiments. But there were a few caveats that were left open. In this paper, we close all of the gaps that we can close. There remain gaps, but those are unlikely to be closed in the near future.”
In the paper, Hangleiter and his colleagues first showed that for these types of sampling tasks the probabilities of all the possible results should be roughly equal, as opposed to being concentrated around a few likely outcomes—in the parlance of math, they showed an “anticoncentration bound.” They then calculated how hard it is to exactly evaluate the average case of one of these simulations.
This result strengthens the argument that quantum computers will always surpass their traditional brethren at these sampling tasks by closing two of the three major loopholes in the theoretical arguments.
Hangleiter has also used complexity theory in developing methods that might be put to more immediately practical use by researchers. His graduate research included work on the Monte Carlo sign problem, some of which was published in the journal Science Advances.
Monte Carlo methods are a way to get very accurate estimates of calculations that are too challenging to tackle with an exact mathematical approach, generally because the sheer amount of data involved makes brute force counting or calculation impractical. While there are multiple different Monte Carlo methods, the general idea is to study a finite number of random samples from a probability distribution instead of keeping track of the exact probability of every possible outcome, and these approaches have been successfully adapted to quantum mechanical problems.
Quantum Monte Carlo methods are powerful tools in quantum computer science but often are plagued by a mathematical nuisance called the sign problem. The sign problem occurs when the values being investigated jump between positive and negative in a messy way that doesn’t allows a useful statistical result to be obtained—for instance, because the answer depends on precisely estimating a tiny difference between two large sums. The poorly behaved fluctuations make determining how the values with different signs cancel out require an impractically large amount of random sampling.
But there is a catch: The sign problem can sometimes be solved just by looking at the computation in a different way. The sign problem is dependent on the mathematical perspective being used, and there are many different ways to approach a computation. Not just for Monte Carlo methods but for any calculation, a mathematician or physicist has to make decisions about how to set up their mathematical perspective: Which way is positive or up? Negative or down? Left? Right? Which point should be the origin (the zero point)?
Such choices of perspective even affect how difficult it is to do a straightforward calculation like finding the average value of a repeating, smooth wave (like the sine wave shown in the graphic, which closely matches the shapes of sound and ocean waves). If you define the middle of the wave as zero so that there are equal amounts of wave above and below, you don’t need mathematical finesse to see that the average is zero. But if you shift the wave up so that the middle no longer lies at zero, the cancellation isn’t as obvious and you have to do a more complex calculation. Or if you consider that flat wave being tilted in a 3D space, you have to account for every point’s orientation in three dimensions. While the calculations required for each choice differ, the final results are all equivalent as long as you understand how to translate between your choices.
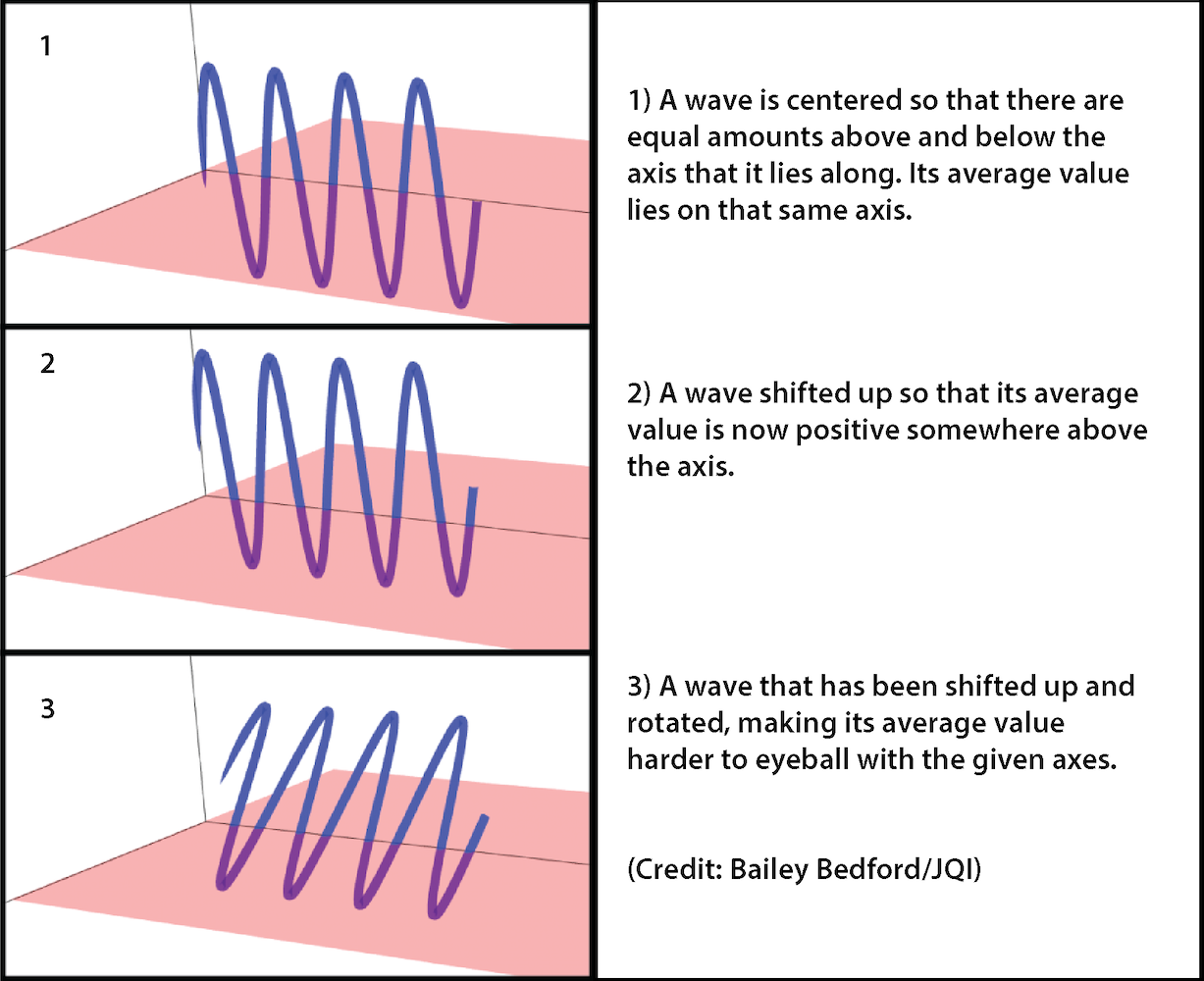
The same flexibility of mathematical definitions can complicate quantum Monte Carlo methods, with the added wrinkle that the math is generally even more difficult—trickier calculations, messier data, problems that aren’t limited to three dimensions, etc. For many of the situations that physicists study using Monte Carlo methods, they need extra mathematical dimensions for every quantum particle involved. This opens many different ways to look at the calculation, and it is often unclear which way is best. Since different approaches to a calculation experience the sign problem to different degrees, it would be useful to be able to judge—or in mathematical terms, measure—the severity for a given set of mathematical decisions.
“This is actually a problem that I've been thinking about since my master’s thesis,” says Hangleiter. “It’s quite difficult, because as it turns out, measuring the sign problem is as hard as simulating the system in the first place. So we really have to find measures for the sign problem, which are maybe not perfect, but which you can efficiently compute. In our work we also develop algorithms for optimizing those measures and assess them using computational complexity theory.”
Hangleiter and colleagues mathematically defined a quantity that corresponds to how bad the sign problem is for a given problem (they called the property the non-stoquasticity). With a rigorous definition in place, they were able to develop a procedure to explore the different possible mathematical perspectives, for certain mathematical settings, and to find the perspective least afflicted with the sign problem. Instead of attempting to find the most elegant solution to the sign problem in a general case their approach can be applied to the sign problem for any quantum Monte Carlo method.
“We want our algorithms to be independent of the physics,” says Hangleiter. “We want a universal method that applies to any model with the sign problem and returns the optimal perspective for a Monte Carlo algorithm.”
Their method does not guarantee that the sign problem can be eliminated, but it provides insight into the nature of the sign problem and is an extra tool for working on these challenging problems. For some cases, where they can’t completely solve the sign problem, just easing it might bring the difficulty down to a level that is practical for state-of-the-art computers to brute force.
“It treads on uncharted territory, because nobody has tried to actually optimize the perspective in which you phrase a problem in the systematic way we did,” says Hangleiter. “So it's unclear how impactful this idea is. It definitely sheds a bit more light on the sign problem and its nature.”
Optimizing quantum Monte Carlo methods and Hangleiter’s other research are part of the research community’s efforts to build a whole new set of tools and to make sure that they don’t waste time enthusiastically banging on a screw with their shiny new hammer. By understanding the underlying nature of quantum computers, researchers are clearing a path towards a future where quantum computers and traditional computers can be put to their best uses. Hangleiter says that during his time at QuICS he wants to interact as much as possible with his colleagues and to get a new perspective on the field of quantum computing that is currently full of grand promises.
“It's a good time to be in the field, because there's a lot of interest,” says Hangleiter. “But I feel like it also comes with quite a responsibility to actually be very transparent about what quantum computers can and can't do on the one hand, and on the other hand to work as a community towards fulfilling the promises we do make.”
Original news story written by Bailey Bedford
November 29, 2021
Prev Next
Connect
Did You Know

UMD is the only major public research university inside the Washington, DC beltway!!
